STM: monoid p wf

STM: sq stable monoid p

ABS: IsGroup(T;op;id;inv)

STM: group p wf

STM: sq stable group p

DIR: grp sig object directory

STM: grp sig inc

STM: comb for grp car wf

STM: grp op l

STM: grp op r

ABS: IMonoid

STM: imon wf

STM: mk imon

STM: imon properties

STM: imon all properties

STM: mon ident

STM: mon assoc

ABS: Mon

STM: mon wf

STM: mk mon

STM: mon properties

STM: assert of mon eq

STM: decidable mon eq

STM: grp eq sym

ABS: IAbMonoid

STM: iabmonoid wf

STM: iabmonoid properties

STM: abmonoid comm

STM: abmonoid ac 1

ABS: AbMon

STM: abmonoid wf

STM: mk abmonoid

STM: abmonoid inc

STM: abmonoid properties

ABS: IGroup

STM: igrp wf

STM: igrp properties

ABS: mk_igrp(T;op;id;inv)

STM: mk igrp wf

STM: grp inverse

STM: grp op cancel l

STM: grp op cancel r

STM: grp inv id

STM: grp inv inv

STM: grp inv assoc

STM: grp inv thru op

STM: grp eq op l

STM: grp eq op r

STM: grp eq shift right

STM: grp inv diff

ABS: Group{i}

STM: grp wf

STM: mk grp

STM: grp properties

ABS: s SubGrp of g

STM: subgrp p wf

ABS: norm_subset_p(g;s)

STM: norm subset p wf

ABS: NormSubGrp{i}(g)

STM: norm subgrp wf

ABS: a  b (mod s in g)

STM: eqv mod subset wf

STM: eqv mod subset is eqv

ABS: IAbGrp{i}

STM: iabgrp wf

STM: iabgrp op inv assoc

STM: iabgrp properties

ABS: |g//h|

ABS: AbGrp

STM: abgrp wf

STM: abgrp properties

ABS: IsMonHom{M1,M2}(f)

STM: monoid hom p wf

ABS: IsMonHomInj(g;h;f)

STM: mon hom inj p wf

ABS: MonHom(M1,M2)

STM: monoid hom wf

STM: sq stable monoid hom p

STM: monoid hom properties

STM: monoid hom id

STM: monoid hom op

STM: grp hom formation

STM: grp hom inv

ABS: InjMonHom(g;h)

STM: inj mon hom wf

STM: inj mon hom properties

STM: ident mon hom shift

STM: inverse grp sig hom shift

STM: mon hom p id

STM: mon hom p comp

STM: tidentity wf for mon hom

STM: compose wf for mon hom

STM: comb for compose wf for mon hom

ABS: gset

STM: dset of mon wf0

STM: dset of mon wf

ABS: OMon

STM: omon wf

STM: omon properties

ABS: OCMon

STM: ocmon wf

STM: ocmon properties

STM: ocmon refl

STM: ocmon trans

STM: ocmon anti sym

STM: ocmon connex

STM: ocmon cancel

STM: ocmon 6

ABS: goset

STM: oset of ocmon wf0

STM: oset of ocmon wf

STM: dset of mon wf2

ABS: a  b

STM: grp leq wf

STM: comb for grp leq wf

STM: sq stable grp leq

ABS: a < b

STM: grp lt wf

STM: comb for grp lt wf

STM: grp leq iff lt or eq

STM: decidable grp lt

STM: grp lt is sp of leq a

STM: grp lt trans

STM: grp lt irreflexivity

STM: grp lt transitivity 2

STM: grp lt transitivity 1

STM: grp leq weakening eq

STM: grp leq weakening lt

STM: grp leq transitivity

STM: omon lt mono imp leq mono

STM: grp leq antisymmetry

STM: grp leq complement

STM: grp lt complement

STM: grp lt trichot

STM: grp op preserves le

STM: grp op preserves lt

ABS: OGrp

STM: ocgrp wf

STM: ocgrp properties

STM: ocgrp inverse

STM: grp leq op l

STM: grp lt op l

STM: grp op polarity

ABS: a < b

STM: grp blt wf

STM: assert of grp blt

STM: grp lt shift right

STM: grp leq shift right

STM: inj into ocmon

ABS: |g|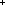

STM: hgrp car wf

STM: hgrp car properties

STM: grp op wf2

STM: grp id wf2

ABS: ghgrp

STM: hgrp of ocgrp wf

STM: hgrp of ocgrp wf2

ABS: 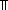(op,id) lb  i < ub. E(i)

STM: itop wf

STM: comb for itop wf

STM: itop aux wf

STM: itop unroll base

STM: itop unroll hi

STM: itop unroll unit

STM: itop unroll lo

STM: itop shift

STM: itop split

ABS: n x(op;id) e

STM: nat op wf

STM: comb for nat op wf

STM: nat op zero

STM: nat op add

ABS: i x(op;id;inv) e

STM: int op wf

STM: comb for int op wf

STM: int op minus

ABS: 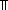 lb  i < ub. E(i)

STM: mon itop wf

STM: comb for mon itop wf

STM: mon itop unroll base

STM: mon itop unroll hi

STM: mon itop unroll unit

STM: mon itop unroll lo

STM: mon itop shift

STM: mon itop split

STM: mon itop split el

STM: mon itop op

ABS: n  e

STM: mon nat op wf

STM: comb for mon nat op wf

STM: mon nat op zero

STM: mon nat op unroll

STM: mon nat op one

STM: mon nat op id

STM: mon nat op op

STM: mon nat op add

STM: mon nat op hom swap

STM: mon nat op mul

ABS: (<o,Id> monoid on T)

STM: comp id mon wf

ABS: <,>

STM: bor mon wf

ABS: <,>

STM: band mon wf

ABS: <+>

STM: int add grp wf

STM: int add grp wf2

ABS: <,+>

STM: nat add mon wf

STM: nat int grp sig hom

STM: nat add mon wf2

STM: nat op mon hom 1

STM: nat op mon hom 2

STM: nat op on nat add mon

ABS: <,*>

STM: int mul mon wf

ABS: when b. p

STM: mon when wf

STM: comb for mon when wf

STM: mon when false

STM: mon when true

STM: mon when of id

STM: mon when thru op

STM: mon when when

STM: mon when swap

STM: mon when is hom

STM: mon when hom swap

STM: nat inc

STM: grp car inc

ABS: zhgrp(n)

STM: int hgrp el wf

ABS: nat(n)

STM: int hgrp to nat wf

STM: zhgrp to nat is hom

STM: zhgrp op mon hom 1

STM: mon nat op wf2

STM: comb for mon nat op wf2

Up

Algebra